Coursera week 6 Machine Learning: Regression (Final)
1. Motivating local fits
이번에는 knn과 kernel regression에 대해 알아볼 것이다.
그전에 fitting 에 대해 알아보자.
fitting 에는 Global fit 과 Local fit이 있다.
우리가 이 때까지 공부했던 것들이 Global fit이라면
아래의 그래프처럼 구간을 나누어 fitting 하는 것을 Local fit이라고 한다.
2. Nearest neighbor regression
knn의 동작 원리는 위와 같다. 말 그대로 가장 가까운 값의 분류값에 속하는 것이다.
내가 배운 책에서는 유클리드 공식을 이용해 거리 계산을 했었는데
여기서는 아직 x 값을 이용해 거리 계산을 한다.
나중에 유클리드 거리 계산이 나올 거 같다..
이 강의에서는 좀 다른 유클리드 거리 계산법을 사용한다.
앞에 weight를 두어 비중을 달리한 거리 계산 법이다.
이것 외에도 위의 사진에 나온 것처럼 여러 계산 방법이 존재한다.
knn은 위와 같은 알고리즘의 형태를 띈다.
여기서 내가 주의 깊게 보고 싶은 것은 알고리즘의 흐름은 이미 알고 있었으나
Dist2NN = Omeaga 로 두고 반복문을 두고 Omega < Dist2NN 이라는 효율적인 부분이다.
알고리즘이 약한 나에게는 이것도 놀라운 부분이었다.
3. k-Nearest neighbors and weighted k-nearest neighbors
위 그림은 k-nn 알고리즘을 나타낸 것이다.
이 알고리즘을 보고 내가 알던 knn과 조금 다르다는 것을 깨달았다..
이제는 weighted k-NN에 대해 알아보자.
cqNN1 같은 변수를 weight라고 하며 가중치를 달리해 정확도를 높인다.
그렇다면 어떻게 weight를 정의할까?
간단하게는 거리가 멀면 weight를 작게 두고
거리가 가까우면 weight를 크게 두는 것이다.
보편적으로는 kernel함수를 사용한다.
위 그래프는 보편적으로 쓰이는 커널 함수들이다.
어떤 커널을 쓸 지 정하는 방법은 위 그래프들의 기울기를 보고 알 수 있다.
가중치를 극과 극으로 쓰고 싶다면 기울기가 가파른 그래프를 사용하면 된다.
이 강의에서는 0으로 수렴되지 않고 기울기도 만만한 가우시안 커널을 사용할 것이다.
위 kernel weight는 인풋이 한 개일때 가능한 kernel 함수이다.
아래는 좀 더 많은 인풋에거 거리를 구하여 kernel 함수를 사용하는 경우이다.
k-nn을 그래프를 이용해 알고리즘을 좀 더 이해해보자.
위 그래프를 잘 이해해야 커널 회귀를 할 때 헷갈리지 않고 잘 할 수 있다.
모든 점에 대해 위와 같은 수행을 하는데
빨간점 차례라고 가정하면,
k개의 Nearest Neighbors를 구하고 그 경계를 노란색으로 그린다.
그리고 k개의 평균을 구한 값이 초록색 점이다.
위와 같은 과정을 모든 점에 대해 수행하면 위처럼 초록색 선이 그려진다.
하지만 위 그래프처럼 discontinuities 라는 문제가 발생한다.
즉, 선이 끊기면서 값들이 수직상승하거나 수직하강하는 점이 있다.
4. Kernel regression
knn에 weight를 부여하는 regression을 kernl regression이라고 한다.
하지만 knn에서 본 weight는 가장 가까운 셋 (Nearst Neighbors)에게만 부여됐다면,
kernel regression은 모든 트레이닝 셋에 weight를 부여한다.
위 그림처럼 모든 트레이닝 셋에 가중치를 부여하는 것을 볼 수 있다.
그리고 전에 본 가우시안 kernel 함수를 통해 가중치를 정한다.
커널 함수를 사용할 때는 2가지에 주의해야한다.
첫번째는 어떤 커널 함수를 사용할 것 인가?
두번째는 어떤 bandwidth lambda 를 사용할 것인가?
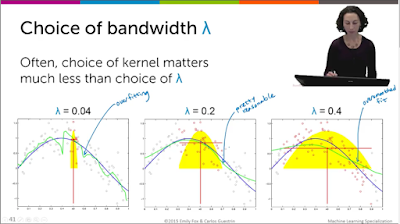
두 가지 중에 람다를 무엇으로 할 지가 굉장히 중요하다.
람다는 전에 공부했던 것과 마찬가지로 bias-variance trade-off를
유의해서 조절해야한다.
위처럼 낮은 람다는 overfitting 을 유발하고 큰 람다는 oversmooth를 유발한다.
다시 쓰지만 그렇다면 람다는 어떻게 정하는가?
역시 cross validation 을 이용하거나 validation set을 이용한다.
5. k-NN and kernel regression wrapup
k-nn과 kernel Regression 은 nonparametric approaches에 속한다.
nonparametric 접근법의 목적은
- Flexibility
- Make few assumptions about f(x)
- 데이터 수가 많을 수록 복잡도 증가
위 그림을 자세히 보면 초록색 선과 파란색 선을 볼 수 있다.
초록색 선은 predict 값이고 파란색 선은 true function이다.
noise가 없다는 가정하에, 비교하고자 하는 것은
1-NN fit 그래프는 처음에 데이터 수가 별로 없을 때는 부정확하다가
많아질수록 복잡도는 증가하고 true function과 거의 똑같아진다.
그에 비해 Quadratic fit은 아무리 데이터 수가 많아져도 true function과
똑같이 될 수 없다는 것을 알 수 있다.
노이즈가 많은 데이터에서, k가 클수록 NN fit 의 MSE 는 0으로 간다.
그래서 true function가 거의 일치하는 선을 갖게 된다.
하지만 knn은 회귀보다 분류에서 더 많이 쓰인다.
7월 25일에 분류 강의가 열리니 그 때까지 회귀 부분을 복습하고 있어야겠다.














댓글
댓글 쓰기