Coursera Machine Learning: Regression Final ( week 1 ~ 3 )

모든 Regression 파트가 끝났다.
다음 파트인 분류를 해야하지만 강의가 아직 열리지 않은 관계로
모든 챕터를 정리하고자 한다.
코세라 회귀 부분을 다 정리하고 이제 youtube에서 DeepLeaning 기초 강의
부분에서 회귀 부분을 공부할 것이다.

WEEK 1

회귀 부분의 시작이다. 

그만큼 기초와 단어에 대해 공부하는 시간이다.

이번 주의 목표는 2가지라고 할 수 있다.

1. ML의 기본 흐름과 기초

2. RSS 의 개념

3. RSS 을 통한 weight 구하기

 3-1. Set Gradient = 0

 3-2. Gradient Descent

1. ML의 기본 흐름과 기초

강의에서는 house pricing 이라는 주제로 회구 파트를 처음부터 끝까지 이어간다.

그래서 위의 기본 개념을 설명할 때 집에 관한 말이 쓰여있다.

y hat , f hat 에 대한 개념을 잘 숙지해야 나중에 헷갈리지 않는다.

y 는 진짜 집 가격이고 y hat 은 내가 예측한 집 가격이다.

중요한 건 x는 y값을 결정하는데 영향을 주는 변수이다.

위 그림에서는 집의 크기라는 변수를 두었다.

변수의 갯수가 많아질수록 차원은 커지고 복잡해진다.

2. RSS 개념

ML에서는 cost를 모두 계산한 함수 RSS 함수가 있다.

Residual sum of squares 의 줄임말이다.

즉, 예측값과 진짜 값의 차이의 제곱을 모두 더한 값을 갖는다.

식으로 보이면 위와 같다.

RSS 는 weight 값들인 w0,w1을 인수로 갖는다.

weight 값들이 많아지면 많아질수록 더 많은 w0,w1,w2,...,wn 까지 갖을 수 있다.

그리고 위의 식 중에 대괄호에 묶인 w0-w1xi가 곧 y hat이다.

직관적으로 보면 yi는 진짜 값이고 대괄호에 묶인 값은 y hat이므로

진짜 값과 예측값을 빼고 있다는 것을 알 수 있다.

3. RSS 을 통한 weight 구하기

Gradient Descent 의 개념을 알기 전에 왜 Gradient Descent를 알아야하는가에

대해 알아야한다.

위에서 공부한 RSS 를 중심으로 weight 값이 w0과 w1 의 값을 구하기 위함이다.

x는 변수의 갯수에 따라 증가하고 그 변수의 영향력에 따른 weight가 존재하는데

weight를 알아야 예측 함수를 구할 수 있지 않겠는가.

위에서 중요한 것은 3차원 그래프이다. 

x 축은 w0 이고 y 축은 w1이고 x와 y의 값에 따라 결정되는 z 축 RSS이다.

RSS는 모든 오차의 합을 뜻하는 것이니 제일 작은 저 빨간 점에 다가갈수록

좋은 예측 함수를 그릴 수 있겠다.

이제는 위의 빨간점에 다가가는 방법에 대해 알아보자.

강의에서는 2가지 방법을 제시한다.

Method 1. Set Gradient = 0

첫번째 방법은 미분만 알면 간단하다.

RSS 벡터에서 w0 에 대한 미분과 w1 에 대한 미분을 한 벡터를 만든 후 equal 0으로

두고 w 에 대한 미분을 w 에 대한 식으로 만드는 것이다.

자세한 것은 위의 식과 블로그에 첫째 주에 정리한 글을 보면 알 수 있다.

Method 2. Gradient Descent

위 내용은 지금 정리한 것만 보고는 이해가 어려울 수 있으니 

전에 week 1에 대해 정리한 것을 보는 것이 좋을 수도 있다.

왼쪽에 있는 그래프는 아까 w0,w1,RSS의 3차원 그래프를 수평으로 짜른 그래프이다.

우리의 목표는 변함없다. 그래프의 가운데 값이 빨간점에 다가가는 것이다.

기본 개념은 3차원 그래프에서 빨간점은 가장 낮은 곳에 있다.

그러므로 기울기를 점점 하강시켜 빨간점에 다가가는 것이 기본 개념이다.

그럼 오른쪽 벡테에 관한 식을 보면,

w0 (t+1) 은 w0 (t) 에서 -n만큼 내려오고 있는 것을 볼 수 있다.

여기서 또 중요한 것은 n이라는 변수이다.

n 은 step size 라고 하는데 얼마만큼 점프할 것인가를 정하는 것이다.

왜 중요하냐면 너무 크게 잡으면 빨간점을 넘어가 버릴 수 있기 때문이다.

그렇다고 너무 작게 잡으면 한참 걸린다.

위 과정을 그림으로 보면 아래와 같다.

 

WEEK 2

이번 주의 목표는 3 가지이다.

1. features, inputs 에 대한 이해와 차이

2. 행렬을 이용해 RSS 표현

3. 행렬을 이용해 gradient 표현

 3-1. Set the gradient = 0

 3-2. Gradient descent

1. features, inputs 에 대한 이해와 차이

생각해보니 내가 정리한 게시글에서 feature 와 input에 대한 

정확한 경계를 쓰지 않고 나 또한 헷갈리게 사용했던 것 같다.

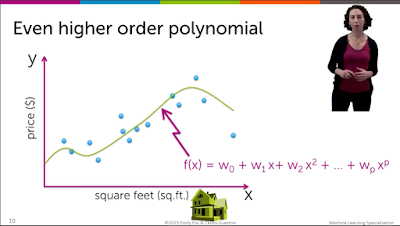
위에서 feature은 x , x^2 , ... , x^p 이라고 할 수 있다.

그러므로 feature 의 수가 많아질수록 차수는 늘어나고 그래프는 더 꼬불꼬불해진다.

그에 반해 input은 sq.ft 처럼 축이라고 할 수 있다.

그러므로 input 이 많아질수록 차원의 수가 늘어나는 것이다.

input과 feature의 차이를 잘 숙지하고 잘 이해하길 바란다.

2. 행렬을 이용해 RSS 표현

이번에는 함수가 아닌 행렬을 이용해 여러가지 식을 표현해볼 것이다.

행렬이 굳이 필요할까라고 생각했지만 파이썬에서 식을 구현할 생각을 하니

행렬 표현이 훨씬 보기 쉽고 구현하기 쉬울 거 같다는 생각이 들었다.

행렬에 대해 정확히 알아야 나중에 텐서플로우나 numpy를 이용할 때 안 헷갈린다.
H 행렬은 N열 D+1 행이고 W 행렬은 D+1열 1행이다.
N은 데이터의 갯수이고 D+1는 feature의 갯수이다.

위 식은 나중에도 계속 나올거기 때문에 꼭 잘 이해하는 것이 좋다.

hT(xi)라고 쓰여진 부분에서 T는 전치행렬을 의미한다.

대각선의 원소들을 기준으로 반전시킨 것이다.

이제 RSS 함수를 행렬로 표현해야한다. 

여기서 알아야 할 것은 A 행렬과 A의 전치행렬을 곱하면 A의 모든 원소들은 제곱값을 가진다.

3. 행렬을 이용해 gradient 표현

Method 1. Set the gradient = 0

w에 관한 행렬식으로 바꾸는 과정을 위 그림에서 설명하고 있다.

행렬의 기본 연산으므로 넘어간다.

Method 2. Gradient descent

1주차에 배운 내용에 위에서 배운 행렬을 넣기만 하면 된다.

WEEK 3

3번째 주의 목표는 3가지이다.

1. 예측 모델 평가

2. 3 measures of loss

3. 3 sources of error

1.  예측 모델 평가

위 그림처럼 트레이닝 셋을 통해 모델링을 해서 fitted function을 만든 후,

예측하고 결정 후 결과를 내는 과정이다.

나중에 테스트 셋을 통해 오류율을 계산하는 것도 나올 것이다.

2. 3 measures of loss

3가지 중 첫번째는 training error 이다.

트레이닝 에러는 내가 예측 모델로 만든 함수와 실제 값과의 차이를 나타낸다.

두번째는 generation error (true error) 이다.

true error 는 정확히 구할 수 없다. 

세상의 모든 변수들을 고려할 수 없기 때문이다.

여하튼 true error는 위와 같은 그래프를 갖는다.

모델 복잡도가 증가할수록 에러가 줄다가 어느 순간 점점 상승한다.

상승하는 시점을 아마 overfitting 이 일어난 순간이라고 할 수 있다.

overfitting 은 나중에 다시 공부할 것이다.

세 번째는 test error이다.

테스트 에러는 나의 예측함수로 테스트 셋으로 시험한 후 에러를 측정한 값이다.

테스트 셋에서 모든 데이터에서의 손실의 평균이라고도 한다.

트레이닝 에러, 테스트 에러, 모델 복잡도에 대해 알아보면 위와 같은 그래프를 가진다.

트레이닝 에러는 모델 복잡도가 증가할수록 감소하고

테스트 에러는 감소하다가 증가하고

트루 에러 또한 감소하다가 증가한다.

우리는 구할 수 없는 true error 를 test error를 통해 유추할 수 있다.

Overfitting 를 에러 그래프를 통해 알아보면  

w^이라는 예측값과 그보다 작은 모델 복잡도를 가진 w`이 있을 때,

1) traning error 관점에서 w^ < w` 

2) true error 관점에서  w^ > w`

이라는 두 조건을 만족시키면 w^은 w`보다 더 overfitting 되어 있다고 한다.

위 사진처럼 트레이닝 셋과 테스트 셋을 분리시켜 트레이닝 시켜야한다.

트레이닝 셋이 더 많고 테스트 셋이 그보다 더 적은게 더 효율적이다.

이 방법은 많은 데이터가 있을 때 좋다. 

하지만 만약 적은 데이터를 갖고 있을 경우 cross validation이라는 방법을 쓰는 것이 좋다.

3. 3 sources of error

예측하는데 3가지 종류의 에러가 존재한다.
하나씩 알아보자.

Part 1 Noise

첫번째는 noise이다.
노이즈는 함수에서 앱실론으로 쓰이며, 현실과 이론의 차이라고 할 수 있을 것 같다.
즉, 더 좋은 모델을 쓴다고 노이즈를 줄일 수도 없다.
이건 노력 밖의 에러니 그냥 이런게 있다고만 알고 가자.
그리고 나머지 두 에러에 집중하자.

Part 2 Bias

f slash(w) 는 여러 다른 트레이닝 셋을 통해 fit 을 한 함수들의 평균 값을 나타낸 선이다.
그리고 최종적으로 Bias 는 True 함수와 slash(w) 함수의 차이이다.
'''Bias 는 '학습 모형이 입력 데이터에 얼마나 의존하는가'를 나타낸다고 할 수 있다.Bias, 즉 선입관이 크면, (좋게 말해서) 줏대가 있고 (나쁘게 말해서) 고집이 세기 때문에 새로운 경험을 해도 거기에 크게 휘둘리지 않는다. 평소 믿음과 다른 결과가 관찰되더라도 한두 번 갖고는 콧방귀도 안 뀌며 생각의 일관성을 중시한다. (High Bias, Low Variance) 반대로 선입관이 작으면, (좋게 말하면) 사고가 유연하고 (나쁘게 말하면) 귀가 얇기 때문에 개별 경험이나 관찰 결과에 크게 의존한다. 새로운 사실이 발견되면 최대한 그걸 받아들이려고 하는 것이다. 그래서 어떤 경험을 했느냐에 따라서 최종 형태가 왔다갔다한다. (High Variance, Low Bias)
''' ( 출처 : http://www.4four.us/article/2010/11/bias-variance-tradeoff)

Part 3 Variance

위와 같이 여러 트레이닝 셋을 통한 polynomial fit 들의 평균은 f slash(w) 처럼 비교적 평평한 그래프를 나타내고 그래프에서 보듯이 variance 의 크기가 엄청 크다는 것을 알 수 있다.
그러므로 높은 복잡도는 결국 높은 variance 를 나타 낼 수 밖에 없다.

part 4 Bias-variance trade-off

위와 같이 MSE를 만들 수 있다. MSE의 가운데 최소값에 다가가는 것이 목표이다.
하지만 우리는 모델을 만들 때 MSE를 구할 수는 없다.
왜냐하면 저 공식의 기반은 True error 여서 구할 수가 없다.
True error를 구할 수 없는 이유는 전에 배웠다.
그러나 나머지 코스를 배우면서 여러 방법으로 bias와 variance 의 트레이드 오프 관계를 최적화하는 방법을 배울 것이다.

위 그래프를 보면 에러와 데이터 수의 상관 관계를 보여준다.
우선 true error 는 데이터 수가 많아질수록 에러는 줄어드는 것을 보여준다.
하지만 bias + noise 값에 수렴할 수 밖에 없다.
아래의 training error 가 위 그래프처럼 아래 부분에서 시작한다면,  데이터 수가 많아질수록 어느 값에 수렴하는 것을 볼 수 있다.