Coursera week 2 Machine Learning: Classification
Learning Linear Classifiers
1. Maximum likelihood estimation
회귀에서 배웠던대로 이번에도 최적의 w hat을 찾아내는 법을 배우는 모듈이다.
w hat을 찾아내는 방법은 validation set을 이용해 정확히 구분해내는
계수를 찾는 방법 밖에 없다.
나중에 gradient ascent 를 배우겠지만 현재는 하나씩 해보며
최적의 계수를 찾는 법을 배운다.
위와 같이 l(w) 함수를 이용한다.
여기서 quality metric을 잘 봐두어야한다.
w 를 최적화시키기 위해 위와 같은 식을 이용한다.
회귀에서는 RSS를 최소화시키는 방법을 이용했지만
분류에서는 l(w)를 최대화시키는 방법을 이용한다.
회귀에서는 RSS를 최소화시키는 방법을 이용했지만
분류에서는 l(w)를 최대화시키는 방법을 이용한다.
data set에 위 식을 이용해 위 식의 값을 가장 극대화시키는 w를 찾는 것이다.
즉, 이미 답이 맞추어져 있는 데이터 셋에 w를 하나씩 계산해가며 가장 좋은 w를 찾는것이다. 예를 들면 , 맞출 확률이 0.9 * 0.9 * 0.8 은 큰 값을 가지며 최적화된 w를 갖고 있는 것이며, 0.1 * 0.2 * 0.4 는 안좋은 w를 값을 가지고 계산해본 것이다.
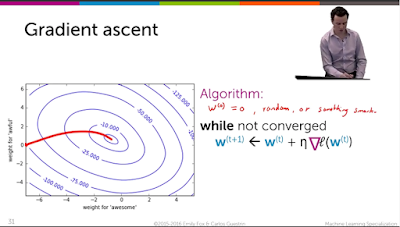
회귀의 gradient descent 와는 다르게 분류에서는 최댓값을 구하는 gradient ascent 를 구한다. 최댓값을 구하는 목적은 위에서 봤듯이 정답일 확률은 큰 것이 좋은 분류기이기 때문이다.
2. Gradient ascent algorithm for learning logistic regression classifier
첫번째 사진의 미분값이 나타내는 것은 l(w) 에 대해 w0,1,2,...,D까지 미분을 수행한 행렬을 보여준다.
좀 더 자세히 알아보자.
위와 같은 식으로 0부터 D까지 만든 미분값을 행렬로 만든 것이다.
이제 예제를 통해 보자.
위 예제를 잘 이해해야한다. w1을 gradient ascent 하는 예제이다.
w1을 l 함수에 대해 미분값을 구하는 과정이다.
미분값을 구하고 스텝 사이즈를 0.1로 정하고 w1의 t+1 은 1.133이 된다.
회귀에서 똑같은 설명을 좀 다르게 설명했다.
회귀에서는 w1을 구할 때 나머지 x값을 다 무시하고 x1만 가지고 계산한다고 했다.
결국 위 과정도 x1만 곱하고 확률을 구해 곱하는 과정이다.
위 그림이 이 때까지 우리가 배운 것을 모두 모아져 있는 알고리즘이다.
tolerance는 말 그대로 관용. 즉, 0으로 딱 떨어질 수 있으면 좋지만 그렇기는 쉽지 않으니 어디까지 봐줄 수 있는가이다.
D+1번 동안 모든 w값들을 반복문을 통해 얻어낸다.
그리고 파란색 글씨인 확률 구하는 식을 통해 미분값을 구한다.
3. Choosing step size for gradient ascent/descent
위 그림은 스텝 사이즈를 너무 크게 하면 안된다는 것을 그래프로 보여준다.
오른쪽 그래프를 보면 초록색 스텝사이즈는 수렴하지 못하고 방황하기만 한다.
위 사진은 optional 강의에 있는 식이다.
l(w) 함수를 로그화시켜서 식을 간단히 하는 것이다.
로그는 더하기만 해도 곱해지기 때문에 식이 간단해진다.
Overfitting & Regularization in Logistic Regression
1. Overfitting in classification
validation set이 overfitting을 측정할 때 중요하다.
위와 같은 구조를 가진다.
트레이닝 셋으로 모델을 트레이닝시키고 최적의 계수를 얻는다.
그리고 validation set으로 overfitting을 평가한다.
회귀 부분에서 이미 다뤘던 내용과 똑같다.
트레이닝 에러는 점점 줄어들고
실제 에러는 줄어들다가 다시 올라간다.
다시 올라가는 부분부터 overfitting이 커진다고 보면 된다.
위 예시는 극단적인 예시이다.
딱 봐도 overfitting이 큰 것을 볼 수 있다.
회귀와 마찬가지로 계수의 크기가 눈에 띄게 큰 것을 볼 수 있다.
2.Overconfident predictions due to overfitting
overfitting 와 계수의 관계를 설명해준다.
회귀에서 공부했듯이 계수가 너무 크면 overfitting 될 확률이 크다.
같이 비율의 weights들도 크기가 엄청 커지면 트레이닝셋에 최적화된 결과를 낳는다.
즉, overfitting이 된다.
3. L2 regularized logistic regression
분류의 cost function에 대해 알아보자.
fit의 크기는 커질수록 좋은 모델이지만 계수의 크기는 커질수록 안좋은 모델이다.
두 가지를 잘 균형있게 맞추는 것이 중요하다.
여기서 주목할 것은 두개의 요소가 서로 상관관계에 있다는 것이다.
적절한 계수의 크기는 fit의 크기를 높여주지만
엄청 큰 계수는 오히려 fit의 크기를 낮춘다.
또한 엄청 낮은 계수도 fit의 크기를 낮춘다.
fit의 크기는 MLE로 측정한다.
MLE는 w의 추정 확률 곱해 최적의 w들을 구하는 것이다.
optional 강의에서는 로그를 통해 MLE 구하는 법을 배웠다.
회귀와 마찬가지로 L2 norm 을 이용해 계수의 크기를 구하고 람다를 통해
조절하는 구조이다.
또한 vaildation set이나 cross-validation 을 통해 람다의 크기를 구한다.
람다의 중요성에 대해 말한다.
람다가 너무 크면 큰 bias 와 작은 variance를 갖게 되고
람다가 너무 작으면 작은 bias 와 큰 variance를 갖게 된다.
즉, 모델 복잡도를 결정한다.
람다가 작으면 모델 복잡도가 커진다.
람다 조절을 통해 cost function의 최적값을 구하는 과정을 Regularization이라고 한다.
그리고 회귀에서 Ridge 와 Lasso의 차이점에서 보았듯이
Ridge는 L2 norm을 사용하고 Lasso 는 L1 norm을 사용하는데
L1 norm을 사용하면 계수가 0으로 가는 속도가 L2 norm 보다 훨씬 빠르고
큰 계수와 작은 계수가 0으로 수렴하는 시간이 비슷한 Ridge에 반해
Lasso 는 큰 계수가 마지막에 0으로 수렴한다.
마찬가지로 logistic regression에서 L2 norm 와 L1 norm을 사용하는데에 차이점이 있다.
L1 norm 은 w 행렬에 0이 많을 때 사용한다.
분류에서는 L1 을 사용하나 L2 를 사용하나 용어 차이는 없는 듯하다.


















댓글
댓글 쓰기