머신러닝 다시 시작하기-2

2. 학습

---

모델을 정했다면 이제 그 모델을 학습시킬 차례다. 학습은 크게 보면 cost function(비용 함수)의 값을 줄이는 과정이다. 그럼 이제 어떻게 cost 값을 정의하고 줄여나가는지 알아보겠다.

2-1) Cost function

---

비용 함수는 정답과 내 머신의 가설을 이용한 예측값을 비교하여 두 값의 차이가 크면 비용을 높이고, 차이가 작으면 비용을 줄이는 함수이다. 비용을 줄이는 쪽으로 파라미터(가중치, $\theta$)를 조절하면 0으로 수렴하는 값을 찾을 수 있을 것이다.

나중에 다시 설명하겠지만 비용 함수를 이용하여 비용 함수의 미분값이 0인 즉, 비용 함수의 최솟값을 찾는 과정을 거친다. 그러기 위해선 비용 함수는 convex-function이어야만 한다. 하지만 회귀 함수의 비용함수를 그대로 분류에 사용하게 되면 non-convex-function이 되기 때문에 이 둘은 비용 함수가 다르다.

2-1-1) Regression Cost function

---

(출처 : https://image.slidesharecdn.com/mlppt-190911145734/95/gradient-descent-algorithm-4-638.jpg?cb=1568214298)

파라미터 벡터 $\theta∈R^{n+1}$에 대하여 비용 함수는 다음과 같이 나타내어진다.모든 파라미터와 모든 트레이닝 셋에 대한 비용함수를 표현한 것이다. $J(\theta) = \frac{1}{2m} \sum_{i=1}^m \left(h_\theta(x^{(i)})-y^{(i)} \right)^2$ 여기서 $h_\theta(x)$는 전에 모델링에서 정의했듯이 아래와 같이 정의된다. $h_\theta(x) =\theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n$ y 값은 정답 값을 의미한다.

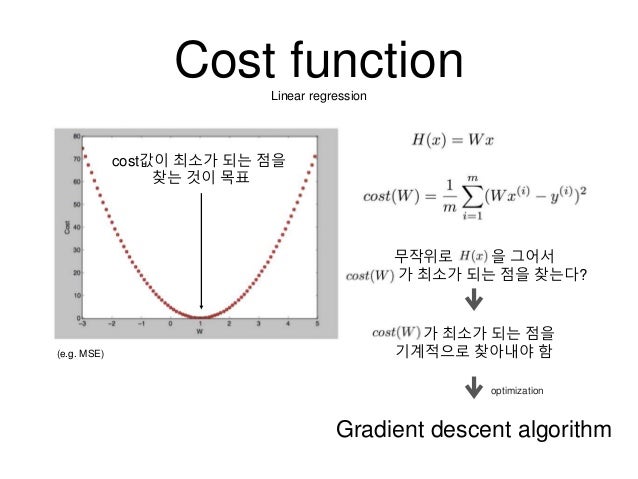
위와 같은 비용 함수를 그래프로 표현하면 아래와 같이 나타나는데, 볼록 함수 형태이다. 그러므로 미분값이 0이 되는 지점이 존재하며 그 지점이 최소값이다. 그 최소값이 가장 높은 정확도를 이끌어내는 것은 아니다. 나중에 설명하겠지만 국지적 최소값에 걸렸을 수도 있기 때문이다.

2-1-2) Logistic Cost Fucntion

---

(출처 : https://wikidocs.net/images/page/4289/logreg403.PNG)

위에서 말했듯이 회귀와는 비용 함수가 다르다. $J(\theta)=\text{cost} \left( h_\theta (x), y \right) =\color{royalblue}{-} y \color{royalblue}{\log\left( h*\theta (x) \right)}\color{salmon}{-} (1-y) \color{salmon}{\log\left( 1-h*\theta (x) \right)}$ 볼록 함수를 만들어 주기 위해 위와 같이 만들어져있다. $h*\theta(x)$는 전에 모델링에서 정의했듯이 아래와 같이 정의된다. $h_{\theta}(x)=\frac{1}{1+\exp(-\theta^{T}x)}$

2-2) Gradient Descent

---

비용 함수를 정의했고, 비용 함수의 값을 줄여나가는 방법에 대해 알아봐야 한다. 그럼 비로소 기계가 학습해서 실전에 쓰일 수 있는 단계가 된 것이다. 비용 함수의 값을 줄이는 방법을 Optimization(최적화)라고 한다. 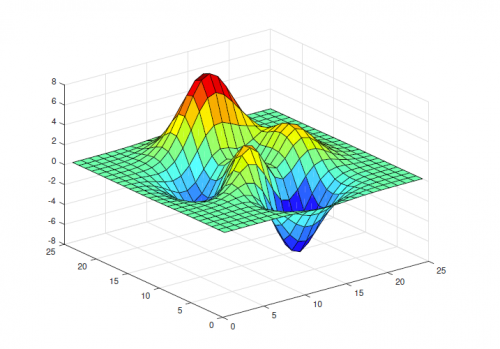(출처 : https://horizon.kias.re.kr/wp-content/uploads/2019/03/Figure_1-500x349.png)

위와 같은 그림에서 파란색으로 된 부분의 최소값으로 향해 가는 방법이다. 즉, $J(\theta)$를 최소화하는 $\theta$의 집합을 찾는 과정이다. 최적화 함수는 회귀와 분류가 같다. 다만, 최적화 함수 내의 가설 함수($h(\theta)$)만 다를 뿐 공식은 같다.

파라미터들을 최적화하는 과정을 수식으로 풀어서 써보면 아래와 같다. $\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, ..., \theta_n) = \theta_j - \alpha\frac{1}{m} \sum*{i=1}^{m} \left( h\_\theta( x^{(i)}) - y^{(i)} \right) x_j^{(i)}$

위 식은 $\theta$ 값을 조절해서 다시 값을 넣어주는 역할을 한다. 그렇다면 어떻게 조절하는가? learning rate값인 $\alpha$과 $J(\theta)$의 미분값 즉, $J(\theta)$의 기울기를 곱하여 기존의 $\theta$에 빼주는 것이다. 이 과정은 최소값을 가질 때까지 반복된다.

최적화 과정을 $\theta_0$부터 $\theta_n$까지 모두 거친다. 여기서 헷갈리지 말아야 할 것은 트레이닝 셋을 한 바퀴 돌면, 비용 함수의 값이 도출되고 파라미터의 집합인 $\theta$의 집합이 수정된다.