머신러닝 다시 시작하기 - 1

앤드류 융 교수님 강의로 다시 머신러닝 공부해볼 계획이다. 우선 머신러닝에 대해 간단히 적어보겠다.
머신 러닝은 크게 아래와 같은 절차를 거친다.

1. [모델링] 데이터를 보고 어떤 모델을 사용할 지 결정한다.
2. [학습] 결정한 모델을 학습시킨다.
3. [평가] 그 모델을 평가한다.

위의 절차는 머신러닝 전과정을 크게 본 것이다. 세부적으로 많은 절차들이 있다. 1번째 요약에서는 세부적인 절차는 다루지 않고 나중에 따로 다루도록 해야겠다.

1. 모델링

데이터를 보고 어떤 모델을 사용할 지 사용자가 결정하여 머신러닝을 시작한다. 머신러닝에 쓰이는 데이터에는 여러 종류가 있다. 크게 2개로 나눈다면, 정답이 있는 데이터와 정답이 없는 데이터로 나누고 싶다. 그에 따라 학습 방법론이 달라진다. 정답이 없는 데이터는 비지도 학습에 쓰이고, 정답이 있는 데이터는 지도 학습에 쓰인다. 굉장히 중요하다.
$X(=Features) \rightarrow h(\theta) (=Hypothesis) \rightarrow Y(=Answers)$
베이스는 위와 같다. 정답인 Y와 내가 예상한 값 h를 비교하면서 $\theta$를 조절하는 과정을 반복한다. 어떻게 반복되는 지는 나중에 더 자세하게 적도록 하겠다.

1-1) 지도 학습

---

지도 학습은 정답(Label)이 있는 데이터를 학습시킬 때 사용된다. 크게 회귀(Regression)과 분류(Logistic Regression = Classification)로 나눌 수 있다.

1-1-1) 회귀(Linear Regression)

회귀는 연속성을 갖는 데이터를 토대로 학습하여 실수면서 연속성을 가진 결과값을 예측할 때 쓰인다.
$h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n$
우리의 예측값 h는 위의 식을 거친다. $\theta$는 머신이 조절해야하는 가중치 값이고, $x$값은 데이터셋의 features의 값이다. 마지막으로 y는 지도학습에서 정답을 담당하는 라벨값이다. 위에서 말했듯이 반복을 돌며 값을 $\theta$집합을 조절한다.

1-1-2) 분류(Logistic Regression)

그에 반해, 분류는 0 혹은 1과 같은 분류 가능한 데이터로 학습하여 이산 값을 도출하는 데에 쓰인다.
분류의 hypothesis는 0과 1 사이의 값만 내보내는 형태가 되도록 하려고 한다.
$h_θ(x)=1/(1+e^{-\theta^Tx})$ 이 함수는 sigmoid function 라고도 불리고, logistic function 이라고도 불린다. 1-1-1) 회귀에서 사용한 $h_θ(x)$를 ${\theta^Tx}$로 두고 새로운 Hypothesis 함수를 만든 것이다.
$y = \begin{cases} 1 \quad if h_\theta(x) \ge 0.5 \\ 0 \quad if h_\theta(x) \le 0.5 \end{cases}$
분류는 0과 1처럼 분류 가능한 값이 도출되어야 하기 때문에 위처럼 기준을 만들어 분류한다.

1-2) 비지도 학습

---

비지도 학습은 정답(Label)이 없는 데이터를 학습시킬 때 사용된다. 데이터가 예쁘면 머신러닝만으로도 충분하지만, 주로 그렇지 않기 때문에 전처리 과정에서 특징이나 구조를 발견하는 데에 쓰인다.

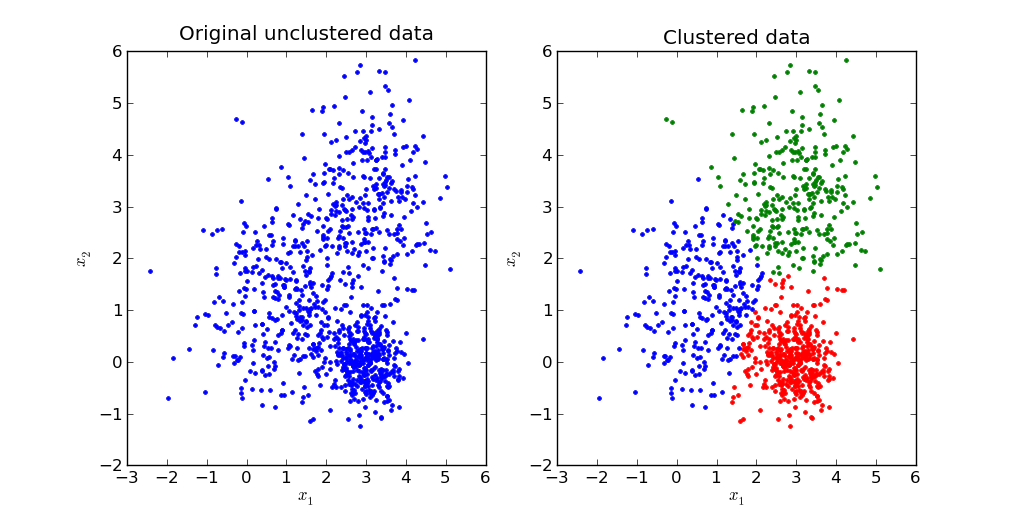
비지도 학습에는 군집화(Clustering), K-평균 알고리즘(k-means) 등이 있다. 지도 학습 내에서 회귀와 분류와는 다르게 알고리즘의 구조에 따라 방법이 다르다.