Machine Learning in Action ch.5.1 & 5.2 Logistic Regression
이번 5장에는 우선 로지스틱 회귀가 무엇인지 배우며, 몇 가지 최적화 알고리즘을 배우게 될 것이다. 최적화 알고리즘을 공부하면서 기울기 상승을 배우게 될 것이며, 확률적 기울기 상승을 조절하는 것에 대해 알게 될 것이다. 이러한 최적화 알고리즘은 분류기를 훈련하는 데 사용된다.


코세라 머신 러닝 공부할 때 다 했던건데 기억이 나질 않는다..
솔직히 영어로 봐서 정확히 다 알진 못했지만 다시 하려니 더 열심히 해놨으면 좋았겠다라는 생각이 들었다.
5.1 로지스틱 회구와 시그모이드 함수로 분류하기 : 다루기 쉬운 계단 함수
위와 같은 그래프를 갖는 함수를 시그모이드 함수라한다.
시그모이드 함수는 우리가 분류 항목을 예측할 수 있는 방정식을 원할 때, 분류 항목이 2개인 경우, 시그모이드 함수는 0 또는 1로 결과값을 출력할 것이다.
시그모이드 함수는 로지스틱 회귀에서 어떻게 쓰일까?
로지스틱 휘귀 분류기를 위해 가지고 있는 각각의 속성에 가중치를 곱한 다음 서로 더한다.
그 결과를 시그모이드에 넣고 0 과 1 사이의 수를 구하게 된다. 이 수가 0.5보다 크면 1로 분류되고 반대면 0으로 분류된다.
5.2 가장 좋은 회귀 계수를 찾기 위해 최적화 사용하기
설명한 시그모이드 함수의 입력은 z 이며, 이 z 는 다음과 같이 주어진다.
z = w0x0 + w1x1 + ... wnxn
x는 데이터이며 , 가장 좋은 계수 w를 찾고자 한다.
이를 위해서는 최적화 이론으로부터 몇 가지를 고려해야만 한다.
우리는 먼저 기울기 상승을 이용한 최적화를 알아볼 것이다.
5.2.1 기울기 상승

기울기 상승 알고리즘은 기울기가 제공한 방향으로 한 단계 이동한다.
기울기 연산자는 항상 크게 증가하는 방향으로 향하게 된다.
이러한 단계는 멈춤 조건에 도달할 때까지 되풀이 된다.
5.2.2 훈련 : 기울기 상승을 사용하여 가장 좋은 매개변수 찾기
def loadDataSet():
dataMat = []; labelMat = []
fr = open('C:/Users/llewyn/Desktop/MLiA_SourceCode/machinelearninginaction/Ch05/testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights
1번째 함수는 loadDataSet() 으로서 텍스트 파일을 열어 모든 줄을 읽는다.
2번째 함수는 sigmoid()으로서 그냥 시그모이드 함수이다.
3번째 함수는 gradAscent()으로서 두 인자를 입력으로 받아 시그모이드 함수를 이용해 가중치를 리턴하는 함수이다.
5.2.3 분석 : 의사결정 경계선 플롯하기
이제 하나의 선을 만드는 데 사용된 가중치의 집합을 해결하고, 분류 항목이 서로 다른 데이터를 분리한다. 어떻게 최적화 절차를 이해하도록 선을 플롯할 수 있을까?
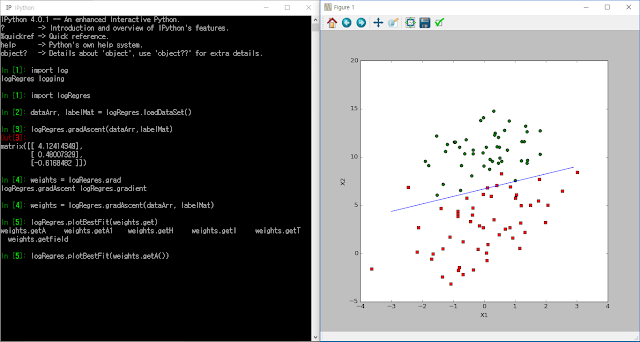
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
분류는 꽤 잘 되었다. 2~4개 정도 잘못된 점들이 있지만 선형 회귀에서 괜찮은 결과라고 생각한다.
5.2.3 훈련 : 확률적인 기울기 상승
확률 기울기 상승 알고리즘은 아래와 같다.
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
변수 h 와 error 가 이제 더 이상 벡터가 아니라 단일 값이란느 것을 제외하고는 확률 기울기 상승은 기울기 상승과 유사하다는 것을 확일 할 수 있다.
흠 .. 결과가 좋지 않다.. 전에 했던 기울기 상승 알고리즘은 괜찮은 결과를 출력했지만
확률 기울기 상승 알고리즘은 그렇지 않은 듯 하다..
문제가 무엇일까..
그래서 우리는 데이터 집합을 200번 반복 실행하도록 수정했다.
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del[dataIndex[randIndex]]
return weights
위 코드 전의 알고리즘과 유사하지만 개선을 위해 두 가지가 추가되었다.
1. alpha 가 매번 변한다. -> 데이터 집합에서 발생하는 높은 빈도의 진동을 개선
2. 가중치를 갱신하는 데 있어 각각의 사례를 임의로 선택한다. -> 주기적인 변화를 줄어들게 함.
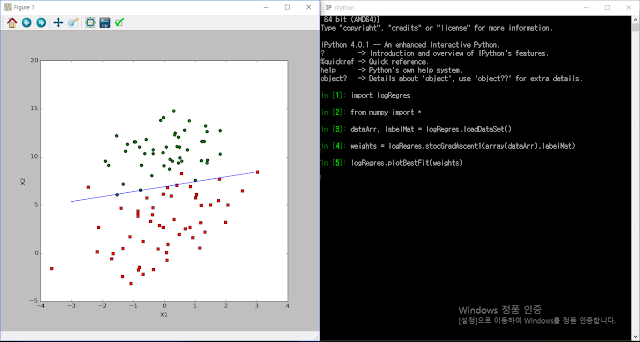
훨씬 더 나은 결과를 출력한 것을 볼 수 있다.
결과는 기울기 상승 알고리즘과 비슷하다고 볼 수 있지만 , 계산은 훨씬 적게 사용하였다.
기울기 상승 알고리즘은 위와 같은 100개의 데이터에서는 효과적일 수 있지만
1억개의 데이터와 같은 큰 데이터에는 확률 기울기 상승 알고리즘이 더 효율적이라는 것을 알 수 있다.


댓글
댓글 쓰기